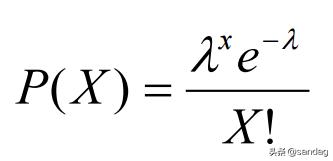数据科学中的常见的6种概率漫衍(Python实现)
|
我们一般糊口中产生的很多常见征象都遵循正态漫衍,譬喻:经济中的收入漫衍,门生的均匀陈诉数目,均匀身高档。另外,中心极限制理声名,在恰当的前提下,大量彼此独立随机变量的均值经恰当尺度化后依漫衍收敛于正态漫衍。 n = np.arange(-50, 50) mean = 0 normal = stats.norm.pdf(n, mean, 10) plt.plot(n, normal) plt.xlabel('Distribution', fontsize=12) plt.ylabel('Probability', fontsize=12) plt.title("Normal Distribution")
可以看出正态漫衍的特性: 曲线在中心对称。 因此,均值,众数和中位数都相称,从而使全部值环绕均值对称漫衍。 漫衍曲线下的面积便是1(全部概率之和必需便是1) 可以行使以下公式得出正态漫衍
行使正态漫衍时,均值和尺度差起着很是重要的浸染。假如我们知道它们的值,通过概率漫衍即可轻松找出猜测准确值的概率。按照正态漫衍的特征,68%的数据位于均值的一个尺度差范畴内,95%的数据位于均值的两个尺度差范畴内,99.7%的数据位于均值的三个尺度差范畴内。
很多呆板进修模子被计划为遵循正态漫衍有最佳结果。以下是一些示例: 高斯朴实贝叶斯分类器 线性鉴别说明 二次鉴别说明 基于最小二乘的回归模子 在某些环境下可以通过对数僻静方根等调动将非正态数据转换为正态情势。 泊松漫衍 泊松漫衍凡是用于查谋变乱也许产生或不产生的频率,还可用于猜测变乱在给按时刻段内也许产生几多次。 譬喻,保险公司常常行使泊松漫衍来举办风险说明(猜测在预按时刻段内产生的车祸事情数),以抉择汽车保险的订价。 当行使泊松漫衍时,我们可以确信产生差异变乱之间的均匀时刻,可是变乱产生简直切时候在时刻上是随机隔断的。 泊松漫衍可以行使以下公式建模,个中λ暗示单元时刻(或单元面积)内随机变乱的均匀产生率。
泊松漫衍的首要特性是: 变乱互相独立 一个变乱可以产生任何次数(在界说的时刻段内) 两个变乱不能同时产生 变乱产生之间的均匀产生率是恒定的。 下图表现了改变λ的值是怎样影响泊松漫衍的: for lambd in range(2, 8, 2): n = np.arange(0, 10) poisson = stats.poisson.pmf(n, lambd) plt.plot(n, poisson, '-o', label="λ = {:f}".format(lambd)) plt.xlabel('Number of Events', fontsize=12) plt.ylabel('Probability', fontsize=12) plt.title("Poisson Distribution varying λ") plt.legend()
指数漫衍 指数漫衍用于对差异变乱之间的时刻举办建模。 举例来说,假设我们在一家餐厅事变,而且但愿猜测差异顾主来就餐的时距离断。针对此类题目行使指数漫衍一个抱负的出发点。指数漫衍的另一个常见应用是保留说明(譬喻装备/呆板的预期寿命)。 指数漫衍由参数λ调理。λ值越大,曲线的斜率变革越快。 for lambd in range(1,10, 3): x = np.arange(0, 15, 0.1) y = 0.1*lambd*np.exp(-0.1*lambd*x) plt.plot(x,y, label="λ = {:f}".format(0.1*lambd)) plt.xlabel('Random Variable', fontsize=12) plt.ylabel('Probability', fontsize=12) plt.title("Exponential Distribution varying λ") (编辑:湖南网) 【声明】本站内容均来自网络,其相关言论仅代表作者个人观点,不代表本站立场。若无意侵犯到您的权利,请及时与联系站长删除相关内容! |