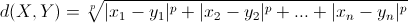基于K－Means的文本聚类

http://blog.csdn.net/freesum/article/details/7376006

作甚聚类

? ? ? ? “聚类是把相似的工具通过静态分类的要领分成差异的组别可能更多的子集（subset）,这样让在统一个子齐集的成员工具都有相似的一些属性。”?? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ——wikipedia

? ? ? ?“聚类说明指将物理或抽象工具的荟萃分构成为由相同的工具构成的多个类的说明进程。它是一种重要的人类举动。聚类是将数据分类到差异的类可能簇这样的一个进程，以是统一个簇中的工具有很大的相似性，而差异簇间的工具有很大的相异性。”

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?——百度百科

? ? ? ? 简朴领略，假如一个数据荟萃包括N个实例，按照某种准则可以将这N个实例分别为m个种别，每个种别中的实例都是相干的，而差异种别之间是区此外也就是不相干的，这个进程就叫聚类了。

聚类进程

? ? ? ? ?1）特性选择(feature selection)：就像其他分类使命一样，特性每每是统统勾当的基本，怎样选取特性来尽也许的表达必要分类的信息是一个重要题目。表达性强的特性将很影响聚类结果。这点在往后的尝试中我会展示。
? ? ? ? ?2）近邻测度(proximity measure)：当选定了实例向量的特性表达后，怎样判定两个实例向量相似呢？这个题目长短常要害的一个题目，在聚类进程中也有着抉择性的意义，由于聚类本质在区分相似与不相似，而近邻测度就是对这种相似性的一种界说。
? ? ? ?3）聚类准则(clustering criterion)：界说了相似性还不足，团结近邻测度，怎样判定相似才是要害。直观领略聚类准则这个观念就是何时聚类，何时不聚类的聚类前提。当我们行使聚类算法举办计较时，怎样聚类是算法体谅的，而聚与否必要一个尺度，聚类准则就是这个尺度。（话说尺度这对象一拿出来，够吓人了吧^_^）
? ? ? ?4）聚类算法(clustering algorithm)：这个对象不消细说了吧，整个进修的重中之重，焦点的对象这里不讲，往后会细说，简朴开个头——操作近邻测度和聚类准则开始聚类的进程。
? ? ? ?5）功效验证(validation of the results)：着实对付PR的作者提出这个进程也放到聚类使命流程中，我认为有点冗余，由于对付验证算法的正确性这事应该放到算法层面吧，可以把4）和5）团结至一层。由于算法正确和有穷的验证自己就是算法的特征嘛。（谁计划了一个算法不得证明啊）
6）(interpretation of the results)：中文版的PR上翻译为功效鉴定，而我感受字面意思就是功效表明。（聚类最终会将数据集分成多少个类，干事前要有原则，干过后要有表明，这个就是表明白。自圆其说也许是较量好的了^_^）

聚类准则

? ? ? ? 聚类准则就是一个分类尺度，对付示例中这样一个数据荟萃，怎样聚类呢。虽然聚类的也许环境有许多。好比，假如我们凭证年级是否为大于1来分类，那么数据集X分为两类：{张三}，{李四，张飞，赵云}；假如凭证班级差异来分，分为两类：{张三，李四}，{张飞，赵云}；假如凭证后果是否合格来分（假设合格为60分），分两类：{张三，李四，赵云}，{张飞}。虽然聚类准则的计划每每是伟大的，就看你想怎么分别了。凭证对分类头脑的几许领略，数据集相等于样本空间，数据实例的特性数（本例共有4个特性[姓名，年级，班级，数学后果]）相等于空间维度，而实例向量对应到空间中的一个点。那么聚类准则就应该是那些神奇的超平面（对应稀有学函数表达式，我小我私人以为这些函数就等同于聚类准则），这些超平面将数据“美满的”分分开了。

聚类特性范例

? ? ? ? 聚类时用到的特性怎样区分呢，有什么范例要求？聚类的特性凭证域分别，可以分为持续的特性和离散特性。个中持续特性对应的界说域是数据空间R的持续子空间，而离散特性对应的是离散子集，其它假如离散特性只包括两个特性值，那么这个离散特性又叫二值特性。 按照特性取值的相对意义又可以将特性分为以下四种：标量的(Nominal)，次序的(Ordinal)，区间标准的(Interval-scaled)以及比率标准的(Ratio-scaled)。个中，标量特性用于编码一类特性的也许状态，好比人的性别，编码为男和女；气候状况编码为阴、晴和雨等。次序特性同标量特性相同，同样是一系列状态的编码，只是对这些编码稍加束缚，即编码次序是故意义的，好比对一道菜，它的特性有{很难吃，难吃，一样平常，好吃，鲜味}几个值来界说状态，可是这些状态是有次序意义的。这类特性我以为就是标量特性的一个特定子集，可能是一个加束缚的标量特性。区间标准特性暗示该特性数值之间的区间故意义而数值的比率有时义，经典例子就是温度，A地的温度（20℃）比B地（15℃）高5度，这里的区间差值是故意义的，但你不能说A地比B地热1/3，这是有时义的。比率特性与此相反，其比率是故意义的，经典例子是重量，C重100g，D重50g，那么C比D重2倍，这是故意义的。（虽然说C比D重50g也是可以的，因此可以以为区间标准是比率标准的一个真子集）。

在常见应用中，包罗我们通常体谅的编程实现中，一样平常只界说nominal特性和numeric特性，个中nominal可以用string来暗示，而numeric可以用number来暗示。（weka中的attribute的特性范例就是这么界说的）！！weka是个好对象WEKA行使教程.pdf

聚类算法的分类

分别要领
? ? ? ?分别要领就是按照用户输入值k把给定工具分成k组（满意2个前提：1. 每个组至少包括一个工具。2. 每个工具必需且只属于一个组），每组都是一个聚类，然后操作轮回再定位技能调动聚类内里的工具，直到客观分别尺度（常成为相似函数，如间隔）最优为止。典范代表：k-means,k-medoids 条理的要领
条理的要领对给定的工具荟萃举办条领略析。分为2类：凝结的和破碎的。凝结的要领也叫自底向上的要领，即一开始将每个工具作为一个单独的簇，然后按照必然尺度举办归并，直到全部工具归并为一个簇或到达终止前提为止。破碎的要领也叫自顶向下的要领，即一开始将全部工具放到一个簇中，然后举办破碎，直到全部工具都成为单独的一个簇或到达终止前提为止。典范代表：CURE,BIRCH
基于密度的要领
? ? ? 基于密度的要领即不绝增添所得到的聚类直到相近（工具）密度高出必然的阀值（如一个聚类中的工具数或一个给定半径内必需包括至少的工具数）为止。典范代表：DBSCAN，OPTICS。
基于网格的要领
? ? ? ? 基于网格的要领即将工具空间分别为有限数量标单位以形成网格布局。全部聚类操纵都在这一网格布局长举办。典范代表：STING。?

基于模子的要领
? ? ? ? 基于模子的要领即为每个聚类假设一个模子，然后凭证模子去发明切合的对像。这样的要领常常基于这样的假设：数据是按照隐藏的概率漫衍天生的。首要有2类：统计学要领和神经收集要领。典范代表：COBWEB，SOMs

作甚k-means

? ? ? ? ?K-means算法是很典范的基于间隔的聚类算法，回收间隔作为相似性的评价指标，即以为两个工具的间隔越近，其相似度就越大。该算法以为簇是由间隔接近的工具构成的，因此把获得紧凑且独立的簇作为最终方针。
　 ? k个初始类聚类中心点的选取对聚类功效具有较大的影响，由于在该算法第一步中是随机的选取恣意k个工具作为初始聚类的中心，初始地代表一个簇。该算法在每次迭代中对数据齐集剩余的每个工具，按照其与各个簇中心的间隔将每个工具从头赋给最近的簇。当考查完全部数据工具后，一次迭代运算完成，新的聚类中心被计较出来。假如在一次迭代前后，J的值没有产生变革，声名算法已经收敛。

算法进程

? ? ? ? 1）从N个文档随机选取K个文档作为质心
　　2）对剩余的每个文得魅丈量其到每个质心的间隔，并把它归到最近的质心的类
　　3）从头计较已经获得的各个类的质心
　　4）迭代2～3步直至新的质心与原质心相称或小于指定阀值，算法竣事
? ? ? ? ?声名如下：起首从n个数据工具恣意选择 k 个工具作为初始聚类中心；而对付所剩下其余工具，则按照它们与这些聚类中心的相似度（间隔），别离将它们分派给与其最相似的（聚类中心所代表的）聚类；然 后再计较每个所获新聚类的聚类中心（该聚类中全部工具的均值）；不绝一再这一进程直到尺度测度函数开始收敛为止。一样平常都回收均方差作为尺度测度函数. k个聚类具有以下特点：各聚类自己尽也许的紧凑，而各聚类之间尽也许的分隔。
　　详细如下：
　　 输入：k,data[n];
　　（1） 选择k个初始中心点，譬喻c[0]=data[0],…c[k-1]=data[k-1]；
　　（2） 对付data[0]….data[n]，别离与c[0]…c[k-1]较量，假定与c[i]差值起码，就标志为i；
　　（3） 对付全部标志为i点，从头计较c[i]={ 全部标志为i的data[j]之和}/标志为i的个数；
　　（4） 一再(2)(3)，直到全部c[i]值的变革小于给定阈值。

k-means 算法弱点

　 ? ?① 在 K-means 算法中 K 是事先给定的，这个 K 值的选定长短常难以预计的。许多时辰，事先并不知道给定的数据集应该分成几多个种别才最吻合。这也是 K-means 算法的一个不敷。有的算法是通过类的自动归并和破碎，获得较为公道的范例数量 K，譬喻 ISODATA 算法。关于 K-means 算法中聚类数量K 值简直定在文献中，是按照方差说明理论，应用殽杂 F 统计量来确定最佳分类数，并应用了恍惚分别熵来验证最佳分类数的正确性。在文献中，行使了一种团结全协方差矩阵的 RPCL 算法，并慢慢删除那些只包括少量实习数据的类。而文献中行使的是一种称为次胜者受罚的竞争进修法则，来自动抉择类的恰当数量。它的头脑是：对每个输入而言，不只竞争得胜单位的权值被批改以顺应输入值，并且对次胜单位回收处罚的要领使之阔别输入值。
　　② 在 K-means 算法中，起首必要按照初始聚类中心来确定一个初始分别，然后对初始分别举办优化。这个初始聚类中心的选择对聚类功效有较大的影响，一旦初始值选择的欠好，也许无法获得有用的聚类功效，这也成为 K-means算法的一个首要题目。对付该题目的办理，很多算法回收遗传算法（GA），譬喻文献 中回收遗传算法（GA）举办初始化，以内部聚类准则作为评价指标。
　　③ 从 K-means 算法框架可以看出，该算法必要不绝地举办样天职类调解，不绝地计较调解后的新的聚类中心，因此当数据量很是大时，算法的时刻开销长短常大的。以是必要对算法的时刻伟大度举办说明、改造，进步算法应用范畴。在文献中从该算法的时刻伟大度举办说明思量，通过必然的相似性准则往复掉聚类中心的侯选集。而在文献中，行使的 K-means 算法是对样本数据举办聚类，无论是初始点的选择照旧一次迭代完成时对数据的调解，都是成立在随机选取的样本数据的基本之上，这样可以进步算法的收敛速率。

作甚TD－IDF

? ? ? ? TD－IDF（term frequency /inverse document frequency)不止一次看到这个观念了，让我印象最深的是吴军在《数学之美》中对这个观念简约的描写。数学之美.pdf
? ? ? ? TF-IDF（term frequency–inverse document frequency）是一种用于资讯检索与资讯探勘的常用加权技能。TF-IDF是一种统计要领，用以评估一字词对付一个文件集或一个语料库中的个中一份文件的重要水平。字词的重要性跟着它在文件中呈现的次数成正比增进，但同时会跟着它在语料库中呈现的频率成反比降落。
? ? ? ? ?TF-IDF算法是成立在这样一个假设之上的：对区别文档最故意义的词语应该是那些在文档中呈现频率高，而在整个文档荟萃的其他文档中呈现频率少的词语，以是假如特性空间坐标系取TF词频作为测度，就可以浮现同类文本的特点。其它思量到单词区别差异类此外手段，TFIDF法以为一个单词呈现的文本频数越小，它区别差异种别文本的手段就越大。因此引入了逆文本频度IDF的观念，以TF和IDF的乘积作为特性空间坐标系的取值测度，并用它完成对权值TF的调解，调解权值的目标在于突出重要单词，克制次要单词。

k-means 的文本聚类

? ? ? ? ?前面先容了TD－IDF我们可以通过用TD－IDF权衡每个单词在文件中的重要水平。假如多个文件，它们的文件中的各个单词的重要水平相似，我就可以嗣魅这些文件是相似的。怎样评价这些文件的相似度呢？一种很天然的设法是用两者的欧几里得间隔来作为相异度，欧几里得间隔的界说如下：

? ? ? 闵可夫斯基间隔：

• TD-IDF的计较
  假设文档荟萃T ＝｛n|tn,n>1｝。
  
  • 对文档举办分词或Tokennize处理赏罚，去掉停用词。
  • 计较各个词呈现的次数freq(wi),则TF(i) = freq(wi)/sum( freq(w1..n)),偶然辰sum( freq(w1..n))可以用max( freq(w1..n))，做归一处理赏罚。
    
  • 统计文件荟萃中有词wj呈现的文件个数doc_freq(wj).则IDF＝ 1/log(doc_freq(wj);
    
  • 按照上面的计较我们可以算出文件i，单词wj的TD－IDF权值W[i][j]= TD(j)*IDF(j)。个中i为文件荟萃T中的一个文件，而j是文件荟萃T中的一个单词。
    通过对文件荟萃T的计较我们可以获得一个二维数组(矩阵)W[i][j].
• K-means聚类的迭代进程
  
  • 1。随机选取k个文件天生k个聚类cluster,k个文件别离对应这k个聚类的聚类中心Mean(cluster) = k ;对应的操纵为从W[i][j]中0～i的范畴内选k行（每一行代表一个样本），别离天生k个聚类，并使得聚类的中心mean为该行。
    
  • 2.对W[i][j]的每一行，别离计较它们与k个聚类中心的间隔（通过欧氏间隔）distance(i,k)。
    
  • 3.对W[i][j]的每一行，别离计较它们最近的一个聚类中心的n(i) = ki。
    
  • 4.判定W[i][j]的每一行所代表的样本是否属于聚类，若全部样本最近的n(i)聚类就是它们的今朝所属的聚类则竣事迭代，不然举办下一步。
    
  • 5.按照n(i) ，将样本i插手到聚类k中，从头计较计较每个聚类中心（去聚类中各个样本的均匀值），调到第2步。

（编辑：湖南网）

【声明】本站内容均来自网络，其相关言论仅代表作者个人观点，不代表本站立场。若无意侵犯到您的权利，请及时与联系站长删除相关内容!